This post is one in a series highlighting MDRC’s methodological work. Contributors discuss the refinement and practical use of research methods being employed across our organization.

Social policy evaluations usually draw inferences using classical statistical methods (also known as frequentist inference). An evaluator may, for example, compare outcomes for program and control groups and make statements about whether estimates are statistically significant.

This approach has two important shortcomings. First, policy evaluators using classical methods typically test a null hypothesis (for example, the hypothesis that the program being studied has no effect). In other words, standard hypothesis tests provide information such as the probability that the estimated effect could have been generated by a program with a true effect of zero. This information is not typically helpful in policymaking. It might instead be useful to know the probability that the program effect exceeds some policy-relevant threshold.

A second drawback of the classical approach is that readers often view results through the lens of their own expectations. A program developer may interpret positive results that are not statistically significant as confirmation of the program’s effectiveness, while a skeptic would interpret with caution statistically significant impact estimates that do not follow theoretical expectations. But a typical classical analysis ignores how people will interpret the findings.

By combining prior beliefs (or priors) about a program’s effectiveness with new data to produce a distribution of impacts (called the posterior distribution), Bayesian statistics provides an alternative that addresses both shortcomings. Many sources of information can inform priors, including results from related studies and expert opinion. When there is little or no information on which to base expectations about the program’s effectiveness, the analysis can use a weakly informative prior, which places similar weight on a wide range of possible outcomes, leading to findings that are based on the new data but allow results to be presented using a distribution of possible effects.

The distribution of effects makes Bayesian analyses more useful for policymaking purposes. Consider two identically designed studies of an employment intervention. Data from the first study show an increase in employment of 6 percentage points while data from the second one show an increase of 5 percentage points. A classical researcher notes that the p-value of the first estimate is 0.05, so the estimated effect is statistically significant, while the p-value of the second is 0.11, indicating the estimate is not statistically significant. In the classical world, the first result would typically receive much more attention than the second even though they differ by only one percentage point. A Bayesian analysis using a weakly informative prior would, by contrast, indicate there is an 94.5 percent probability that the impact is positive in the second study and a 97.5 percent probability that the impact is positive in the first study. The Bayesian analysis would thus favor the first finding, but the difference between them would be presented as relatively small, as seems reasonable when the estimates differ by only one percentage point.

Because the prior is combined with new data in conducting the statistical analysis, a strong prior — such as good research on the likely effects of an intervention — allows Bayesian analyses to provide more precise estimates, so a new study can be smaller than if it must stand alone. This also provides a way of guarding against large spurious findings, which are more likely to happen in small studies. In the Bayesian framework, information from the new data will be pulled toward the prior to a degree that depends on the precision of the prior and the precision of the new data. That means it is important to use a valid prior; results will be misleading if an incorrect prior is used. One solution is to use a range of priors, some more optimistic than others and some more precise than others, to see how sensitive the results are to assumptions about the prior information.[1]

Bayesian methods are relatively uncommon in social policy evaluations, but they are becoming more popular. They have been used in a few ways:

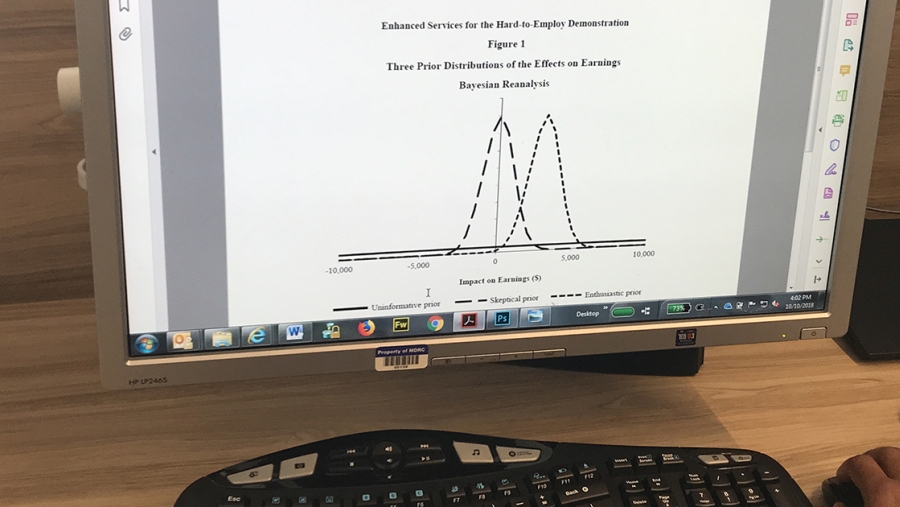
• To estimate full-sample impacts. Bayesian updating has been used in assessing an intervention’s likely effects. Michalopoulos (2012) provides an example in its reanalysis of results from a set of random assignment studies that formed the Enhanced Services for the Hard-to-Employ Demonstration and Evaluation Project. The Bayesian reanalysis presented a more positive take on one of the study’s findings, in part because of the presentation of results in terms of probabilities and in part because the positive results from prior studies increased confidence in small effects that did not achieve statistical significance.

• To estimate effects for subgroups or sites. In examining the impacts of a multisite intervention (the Infant Health and Development Program) by site, Gelman, Hill, and Yajima (2012) show how Bayesian methods can be used to develop site estimates that are more precise than under classical methods: So-called shrinkage estimators result in site estimates that are pulled toward a common estimate, which is typically the estimate for all sites combined.[2] The degree to which a site’s estimate will be pulled toward the common estimate depends on the uncertainty of the estimate of that site, which usually depends primarily on the site’s sample size.

• To develop Bayesian adaptive designs, which allow for adjustment of random assignment as the evidence of a treatment’s effectiveness builds. Most applications of this method to date have been in biomedical research studying multiple treatment arms. Using this approach, the study begins by randomly assigning individuals to different treatment arms based on a predetermined ratio, such as an equal number of people in each treatment arm. As people receive the interventions, their outcomes are combined with a prior to form a posterior distribution of the relative effectiveness of the different treatments. Random assignment is adjusted over time so that treatments that look more effective are assigned more people and those that look less effective are assigned fewer people. This can quickly shut down treatment arms that are ineffective — or end randomization where a treatment has enough evidence of effectiveness. Compared with a multi-arm study that has fixed random assignment ratios to the different treatments, a Bayesian adaptive design can result in fewer participants being involved in the study overall, since assigning more people to effective treatments results in faster evidence of effectiveness, and fewer people are assigned to the less effective treatments.

Given that a Bayesian approach can provide a more efficient way of conducting research and lead to results that are easier to use in making policy decisions, why are these methods rarely used in social policy evaluations? One reason is lack of familiarity. Most researchers are trained in classical methods, and most consumers of evaluation research are used to the presentation and language of classical methods. A second concern is that it can be difficult to develop reasonable priors and even more difficult to develop priors that would be agreed to by different people. Bayesian methods can consequently appear to be unduly subjective, although the approach of presenting results with a range of priors can make transparent the role the prior plays in the final findings. These problems can be overcome, as they have been to some extent in biomedical research, where Bayesian methods are much more common.

At the same time, it is important to recognize that there are non-Bayesian analogues of some of the examples discussed in this post. Meta-analysts use classical methods to combine data from prior studies with new data to provide results that can be more precise and more informative than any single study, and adaptive designs are not solely a Bayesian endeavor.[3] Likewise, shrinkage estimators and adaptive designs exist in both Bayesian and classical varieties.[4] This suggests the gap between Bayesian and classical methods is smaller than sometimes imagined.